L-Systems

L-Systems originated from the observations of micro flora growth patterns. The patterns allowed for forms of symmetry and growth through the use of rules. The L-Systems used in this post will utilize two main parts: the vocabulary and the axiom. The vocabulary is the apparent commands and the rule on iteration involving them. The Axiom is the initial set of vocabulary that will grow the entire system.
Note that almost all commands will be using the Processing turtle library. All documentation and installation are provided in the linked site.

Task 1: Turtle and Processing

This task is split into 4 objectives to utalize the turtle library: draw both a using commands “I” and a “T”, draw a triangle, draw an equilateral pentagon, draw a uniform circle. One objectice to note for all of these commands is that the turtle should not overlap on any previously drawn lines for the specific command. If the turtle is going to backtrack, it should not draw over the same line again.

import Turtle.*;
Turtle t;
import processing.pdf.*;
import processing.svg.*;
String fileName;

void setup() {
  size(500,500);
  background(255);
  stroke(0);
  t = new Turtle(this);
  noLoop();//only use draw once
}

Objective 1

float scale = 1.0;

void letter_I(float x, float y, Turtle t, float line_length)
{
  t.setX(x);
  t.setY(y);
  t.setHeading(0);
  
  //starting the letter
  t.push();
  t.left(90.0);
  t.forward(line_length*scale);
  t.penUp();
  t.right(180.0);
  t.forward(line_length*scale);
  t.penDown();
  t.forward(line_length*scale);
  t.pop();
  
  t.right(180.0);
  t.forward(2*line_length*scale);
  
  t.push();
  t.left(90.0);
  t.forward(line_length*scale);
  t.penUp();
  t.right(180.0);
  t.forward(line_length*scale);
  t.penDown();
  t.forward(line_length*scale);
  t.pop();
}

void letter_T(float x, float y, Turtle t, float line_length)
{
  t.setX(x);
  t.setY(y);
  t.setHeading(0);
  
  //starting the letter
  t.push();
  t.right(180.0);
  t.forward(line_length*2*scale);
  t.pop();
  t.right(90.0);
  t.forward(line_length*scale);
  t.right(180.0);
  t.penUp();
  t.forward(line_length*scale);
  t.penDown();
  t.forward(line_length*scale);
  
}

Objective 2

void shape(float x, float y, Turtle t, float line_length, int sides)
{
t.setX(x);
t.setY(y);
t.setHeading(0.0);
float angle = 360 / (float)sides;

for(int i = 0; i < sides; i++)
{
t.forward(line_length);
t.right(angle);
}
}

Objective 3

The function to generate the equilateral pentagon will be the same as the function for the triangle, just with a larger side count. Therefore the only displayed code will be the draw function.

Objective 4

As stated with objective 3, the same function for the triangle was utilized for this command as well.

Task 2: L-System Framework

This class will be the basis for all the custom classes. Some areas of the code require “TODO’s” to become functional. after the rules are displayed, all the TODO’s will be displayed.

lSys Initialization call in Setup:
//lSys = initSquare();
lSys = Forrest();//Genome, Forrest, Metro, Run4 

Iterations call in draw: 
for(int i = 0; i < numIterations; i++)
{
   println(i);
   lSys.iterate();
}

Replacing Characters in the iterate function:
for(int i = 0; i < current.length(); i++)
{
  char rule = current.charAt(i);
  String temp = rules.get(rule);
      
  //check if it is a null
  if(temp == null)
  {
    temp = str(rule);
  }
  currentIterationBuffer.append(temp);
}

The TODO of implementing the directions for each vocabulary item, will be described in Task 3. As the custom inscrtuction will be described there as to depict the adjacent rules.

After all the TODO’s are done, the L-system can be drawn and iterated upon in real time. Below is a representation of the first 4 generation.

Task 3: Unique L-Systems

The Instructions used

F – Move forward by the preset distance
B – Move backwards by the preset distance
+ – Turn right by 90 degrees
– – Turn left by 90 degrees
, – Turn right by 45 degrees
. – Turn left by 45 degrees
[ – Push the turtle data into a memory stack
] – Return to the highest level push availiable
E – Produce a half a square on the right side of the line, then return to the initial point
Q – Produce a half a square on the left side of the line, then return to the initial point
C – Set the stroke color to reprent a full cut by the laser cutter
V – Set the stroke color to reprent a vector cut by the laser cutter
‘ ‘(Space) – A spacing marker to make reading inputs easier

As most of the code is similar, the new mechanics will be shown imediatly, then each L-System will only display the axiom and rules; for the sake of brevity.

public void iterate() {
    // get a copy of the current iteration string
    String current = this.getIterationString();
    
    // Now clear the current interation string
    this.clearCurrentStringBuffer();

    for(int i = 0; i < current.length(); i++)
    {
      char rule = current.charAt(i);
      String temp = rules.get(rule);
      
      //check if it is a null
      if(temp == null)
      {
        temp = str(rule);
      }
      currentIterationBuffer.append(temp);
    }
 
     // Increment our iteration after we are done
     iterationNum += 1;
  }

for (int i = 0; i < currentIteration.length(); i++) {
      Character c = currentIteration.charAt(i); 
      // [TODO]: Implement different l-system vocabulary
      switch (c) {
        case 'F':
          t.forward(dist);
          break; // The "break" exits out of the switch statement and prevents the next cases from running
       case 'B':
         t.back(dist);
         break;
       case '+':
         t.right(rotateAngle);
         break;
       case '-':
         t.left(rotateAngle);
         break;
       case '[':
         t.push();
         break;
       case ']':
         t.pop();
         break;
       
       //============== custom functions ==============
       case 'E':
         t.push();
         t.right(rotateAngle/2);
         t.forward(dist*cos(dist*cos(PI/4)));
         t.right(rotateAngle);
         t.forward(dist*cos(dist*cos(PI/4)));
         t.pop();
         break;
       case 'Q':
         t.push();
         t.left(rotateAngle/2);
         t.forward(dist*cos(dist*cos(PI/4)));
         t.left(rotateAngle);
         t.forward(dist*cos(dist*cos(PI/4)));
         t.pop();
         break;
       case ',':
         t.right(rotateAngle/2);
         break;
       case '.':
         t.left(rotateAngle/2);
         break;
       case 'C':
         stroke(cut);
         break;
       case 'V':
         stroke(vector);
         break;
       case ' '://I just want to seperate things better...
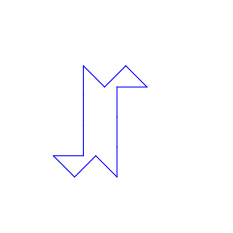
         break;

Design 1: “Genome“

I named this funcition after the pseudo-helixes that the system starts to make and how the color scheme remids me of how DNA was depicted in early 2000’s meia.

Axiom:
V F+F,B+ F+F,BB++ F+F,B+ F+F,BB++
Rules:
F = F[C.B.V]F
B = B[C,F,V]B
+ = ,F+B
– = .B-F

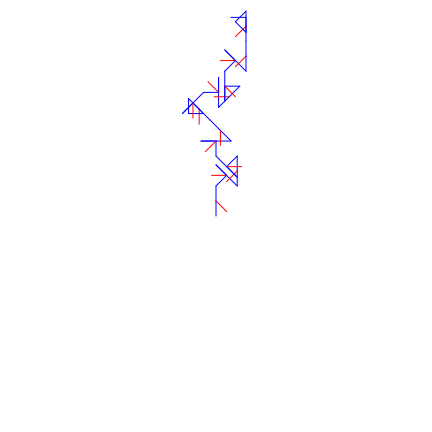
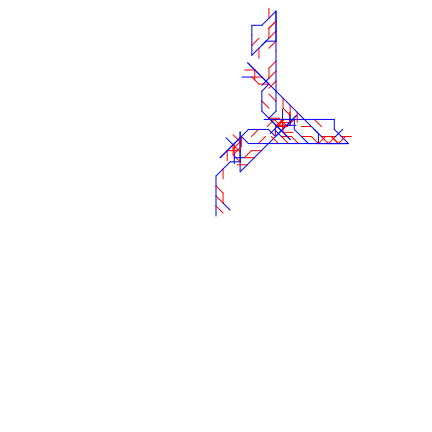
Design 2: “Forrest”

The method of population by the L-System reminded me of an anecdote of how the old tres of the forrest support and grow new trees when they fall. also the general shape of this system being that of a pine.

Axiom:
V FF
Rules:
F = F[C[,B].BV]F
B = B[+F]B

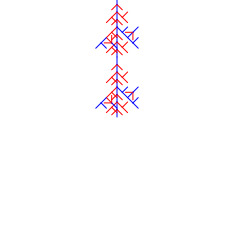
Design 3: “Metro”

Through the use of the colors and the jumbled mess is becomes, I am reminded of my first time in New York City seeing the sprawling subway metro lines and being both amazed and over stimulated.

Axiom:
V F[,][.]F
Rules:
F = F[,][.]F
, = FF[,+F].-F
. = .FF[,+F].-F
] = [CF+F-F]]
[ = [V
V = C
C = V

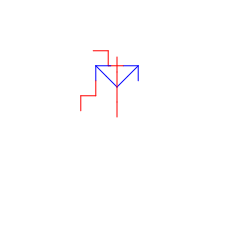
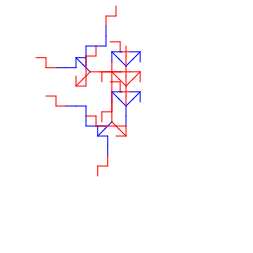
Task 4: Laser Cutting

As with the last Comp Fab assignment, all laser cutting was done at the CU Boulder BTU Lab. All material used was scrap cardboard I had lying around.
Though the initial plan was to use both vector etches and full cuts. After some review of the L-systems to be cut, I realized that much of the design would be lost due to the cuts removing a large portion of the vectors.

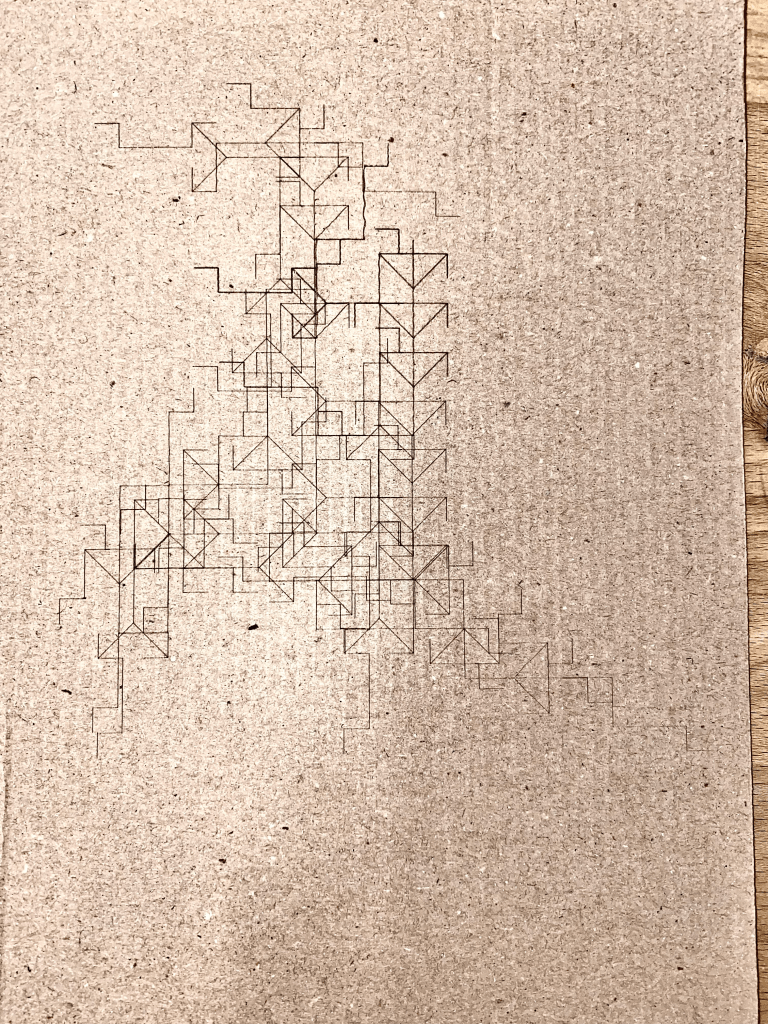
Conclusion

The iterative nature of L-Systems, allows for interesting growth patterns and symmetry. The basis from plant growth can be seen in some of the systems created in this post. This action of controlling the turtle to take specific steps in a specified order will later be built upon to allow for the splitting and slicing of 3D objects into 2D planes that can be interpreted by printers.